本文记录学习深度学习过程,记录一些重点和难理解的方面吧,非总结向,可能不是很全面。
参考书目《Deep Learning》–Ian Goodfellow
[TOC]
第1章 引言
1.1 本书面向的读者
1.2 深度学习的历史趋势
第1部分 应用数学与机器学习基础
第2章 线性代数
2.1 标量、向量、矩阵和张量
这一部分第一次接触,看起来很像是之前数学、物理中学过的概念,但是琢磨一下还是发现概念很绕的,总是似懂非懂,脑子转不过弯,网上看了很多介绍,千篇一律,都只是讲概念。
Youtube上有一段Dan Fleisch讲解张量的一段视频,是人们非常推荐的。
可能因为我脑子笨吧,看了这么生动的讲解还是没有了解。所以又找了一些资料,看看是否有更通俗的理解。
张量就是一个变化量。
张量有零阶、一阶、二阶、三阶、四阶等等。
零阶张量是标量(数值)
一阶张量是向量(数值和方向的组合)
二阶张量是矩阵(向量的组合)
三阶张量是数据立体(矩阵的组合)
四阶张量(数据立体的组合)
等等。
1、标量就是一个数值,可以看成是一个数值上的变化量。
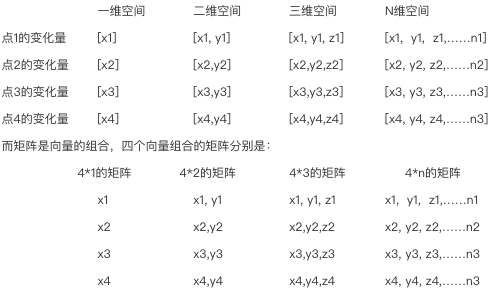
2、向量是点到点的变化量,而点可以是一维空间上的点、二维空间上的点、三维空间上的点,等等。
一维空间上的点的变化,好像点(x)在线上的移动,也即是左右的线性变化,变化量可以表示为[x1]。
二维空间上的点的变化,好像点(x,y)在面上的移动,也即是前后左右的线性变化,变化量可以表示为[x1, y1]。
三维空间上的点的变化,好像点(x,y,z)在体上的移动,也即是前后上下左右的线性变化,变化量可以表示为[x1, y1, z1]。
N维空间上的点的变化,好像点(x,y,z,…..n)在体上的移动,也即是2n个方向的线性变化,变化量可以表示为[x1, y1, z1,……n1]。
3、矩阵是图形到图形的变化量,而图形可以是一维的线、二维的面、三维的体,等等。
3.1、一维的线的变化,我们知道两点可以表示一线段,则需要用两个向量组成的矩阵对两点进行变化,就能达到对线段的变化。

3.2、二维的面的变化,我们知道三点可以表示一个三角形,四点可以表示一个四边形,五点可以表示一个五边形,等等。就拿三角形来说,需要用三个向量组成的矩阵对三点进行变化,就能达到对三角形的变化。

3.3、三维的体的变化,我们知道4点可以表示一个三角堆,5点可以表示四棱锥、6点可以表示一个三棱柱,等等。就拿三角堆来说,需要用四个向量组成的矩阵来对四个顶点进行变化,就能达到对三角堆的变化。
4、三阶张量可以表示图像的变化量,图像与图形的不同是图像的点除了有坐标,还具有颜色特性,如RGB、RGBA、YCbcr等表示的颜色。拿RGB的图像来说,它的变化量包括坐标和色值变化。图像坐标的变化相当于图形的变化,即是一个矩阵的变化。色值变化也就是RGB在颜色空间中的一个点变化,也是一个矩阵的变化,图像变化有两个矩阵变化,三阶张量是矩阵的组合,则可以用三阶张量来表示图像的变化量,如tensor[3,5,5]表示3颜色通道的5*5大小图形的变化量。
5、四阶张量在TensorFlow的神经卷积网络中,经常用到。下面举个例子。
5.1、输入张量格式:[batch, in_height, in_width, in_channels]
5.2、卷积核格式:[filter_height, filter_width, in_channels, out_channels]
5.3、我们来对输入图片进行卷积得到特征图片。
一张5通道的5*5的输入图片:input = [1, 5, 5, 5];
5输入通道、7输出通道的3*3大小的卷积核:filter = [3, 3, 5, 7];
strides=[1,1,1,1]表示各个方向步长为1;
padding=“SAME”表示卷积核遍历到输入图片的每个像素,得到的特征图片与输入图片是一样大小。
tf.shape(tf.nn.conv2d(input, filter, strides=[1,1,1,1], padding=“SAME”));
卷积结果是:[1, 5, 5, 7]
5.4、用图形来表示上面的卷积过程。

简化版:
标量,向量,矩阵与张量
1、标量
一个标量就是一个单独的数,一般用小写的的变量名称表示。
2、向量
一个向量就是一列数,这些数是有序排列的。用过次序中的索引,我们可以确定每个单独的数。通常会赋予向量粗体的小写名称。当我们需要明确表示向量中的元素时,我们会将元素排列成一个方括号包围的纵柱:
我们可以把向量看作空间中的点,每个元素是不同的坐标轴上的坐标。
$$
x=[x_1\ x_2\ \cdots\ x_n]
$$
3、矩阵
矩阵是二维数组,其中的每一个元素被两个索引而非一个所确定。我们通常会赋予矩阵粗体的大写变量名称,比如A。 如果一个实数矩阵高度为m,宽度为n,那么我们说 。
$$
A=
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \
a_{21} & a_{22} & \cdots & a_{2n} \
a_{31} & a_{32} & \cdots & a_{3n} \
\cdots & \cdots & & \cdots \
a_{m1} & a_{n2} & \cdots & a_{mn} \
\end{bmatrix}
$$
矩阵这东西在机器学习中就不要太重要了!实际上,如果我们现在有N个用户的数据,每条数据含有M个特征,那其实它对应的就是一个NM的矩阵呀;再比如,一张图由1616的像素点组成,那这就是一个16*16的矩阵了。现在才发现,我们大一学的矩阵原理原来这么的有用!要是当时老师讲课的时候先普及一下,也不至于很多同学学矩阵的时候觉得莫名其妙了。
4、张量
几何代数中定义的张量是基于向量和矩阵的推广,通俗一点理解的话,我们可以将标量视为零阶张量,矢量视为一阶张量,那么矩阵就是二阶张量。
例如,可以将任意一张彩色图片表示成一个三阶张量,三个维度分别是图片的高度、宽度和色彩数据。将这张图用张量表示出来,就是最下方的那张表格:
其中表的横轴表示图片的宽度值,这里只截取0319;表的纵轴表示图片的高度值,这里只截取04;表格中每个方格代表一个像素点,比如第一行第一列的表格数据为[1.0,1.0,1.0],代表的就是RGB三原色在图片的这个位置的取值情况(即R=1.0,G=1.0,B=1.0)。
当然我们还可以将这一定义继续扩展,即:我们可以用四阶张量表示一个包含多张图片的数据集,这四个维度分别是:图片在数据集中的编号,图片高度、宽度,以及色彩数据。
还有一种描述
- (2,3) 表示两个一维数组,每个一维数组长度为3
- (2,3,4) 表示两个二维数组,每个二维数组有3个一维数组,每个一维数组长度为4
- (2,3,4,5) 表示两个三维数组,每个三维数组有3个二维数组,每个二维数组有4个一维数组,一维数组长度为5
可能更容易理解。
